106年推甄通訊所心得(下)
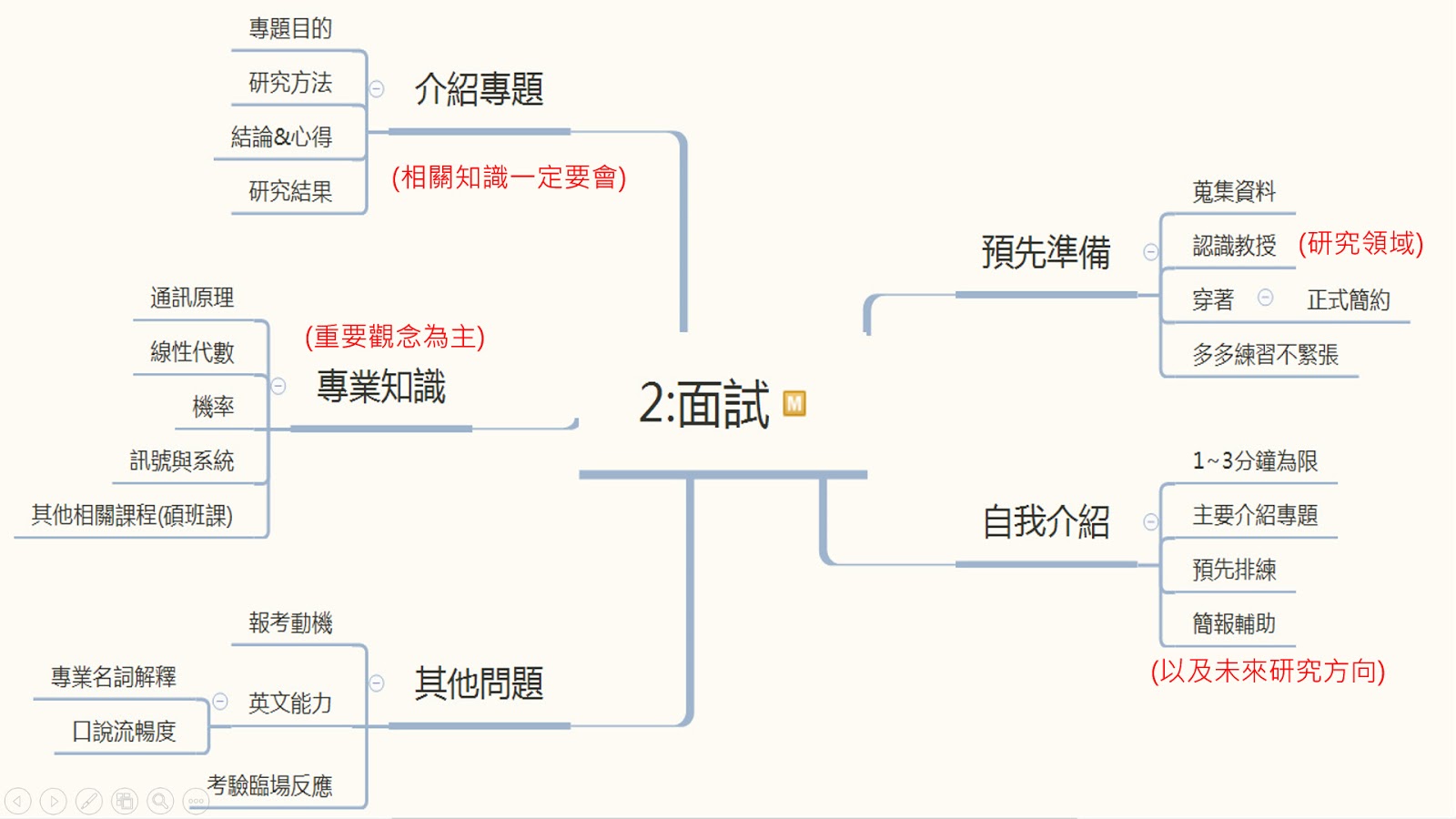
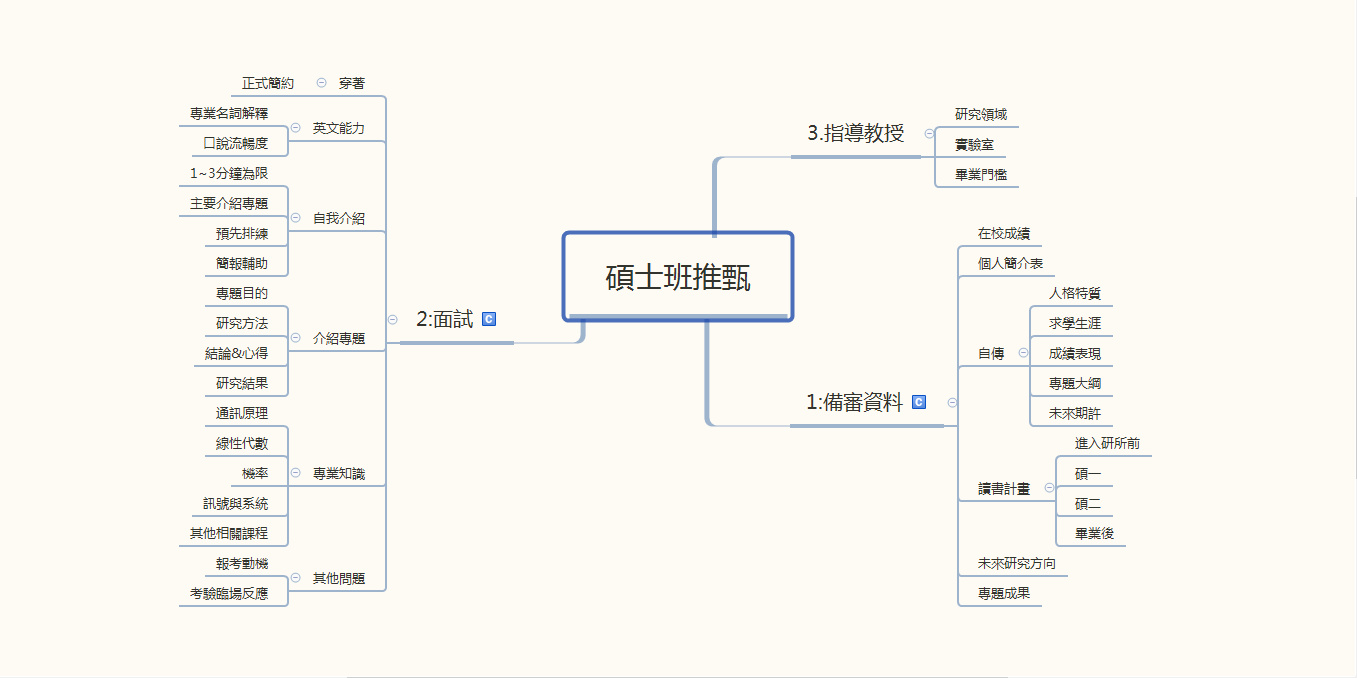
恭喜學弟妹們通過第一階段的審查,不過在此時才是推甄真正的考驗.接續上一篇的主題,這次來跟大家分享研究所面試的心得. 本篇文主要包括了在大學畢業前於系上舉辦的考研分享會的內容,並再多補充些當時時間有限,未能在分享會上提及的小技巧. 若覺得這篇文章對你們有幫助&有任何問題的話,請不吝在此篇文章下支持&留言,並分享給其他有需要的同學們. 跟之前上篇一樣,就以這張心智圖來概括講解面試的注意事項吧~~! 預先準備:準備甚麼? 在接到面試通知時,你就必須開始計畫好當天面試的細節.若是面試地點需要通勤前往,就要提前準備訂好來回車票甚至是要下榻的飯店住宿; 若是面試好幾間學校,更要注意是否有學校科系撞期?若有的話就要趕緊打電話至學校系辦調換時間(例如:上午場改換成下午場)或是找人替換順序,確保不會有錯過面試時間,或是使自己太趕來不及在面試下一個科系時, 擁有最好的狀態 . 以去年為例,當時中央通訊跟成大電通所面試恰巧在同一天,若你沒及時找到人可調換順位或上下午場,一天南北來往的時間可是會非常緊湊. 接著就是要好好準備面試會問的問題了.推甄面試會問到的問題,大致上可以分成這幾類: (1)自我介紹 自我介紹無論是研究所面試,就算未來應徵正職工作時也是必定常問的題目,所以一定要多多練習,時間控制在1~3分鐘之內.推甄時的自我介紹主要是講述你的 名字,學校,科系,以及專題 ,這是教授比較想聽到的內容.講這些時間也大概3分鐘內跑不掉了.假如講完還有多餘的時間,可以再講述你 未來想研究的方向 .關於這點本文等等還會提及到 (2)專題內容 誠如(1)所述,就算你自我介紹沒提及到專題內容,教授也一定會想問你在大學時的研究為何, 所以專題可說是必須要清楚不過的東西. 專題算是大學生涯裡不容忽視的項目,它代表了學生的研究技巧&解決問題的能力, 關於構思問題、蒐集資料、分析、並且撰寫的學問,類似「大學畢業論文」,若要推甄研究所除了課業成績優秀之外,就是要顧專題研究 你可以藉由這些問題來判斷你對專題的了解有多少: 能否7句話以內的篇幅來描述你的專題內容? 專題研究是用甚麼方法? 專題的結果是甚麼? 此結果符合你的問題模型嗎?有沒有不合理的地方? 你對這專題有甚麼心得嗎? ...