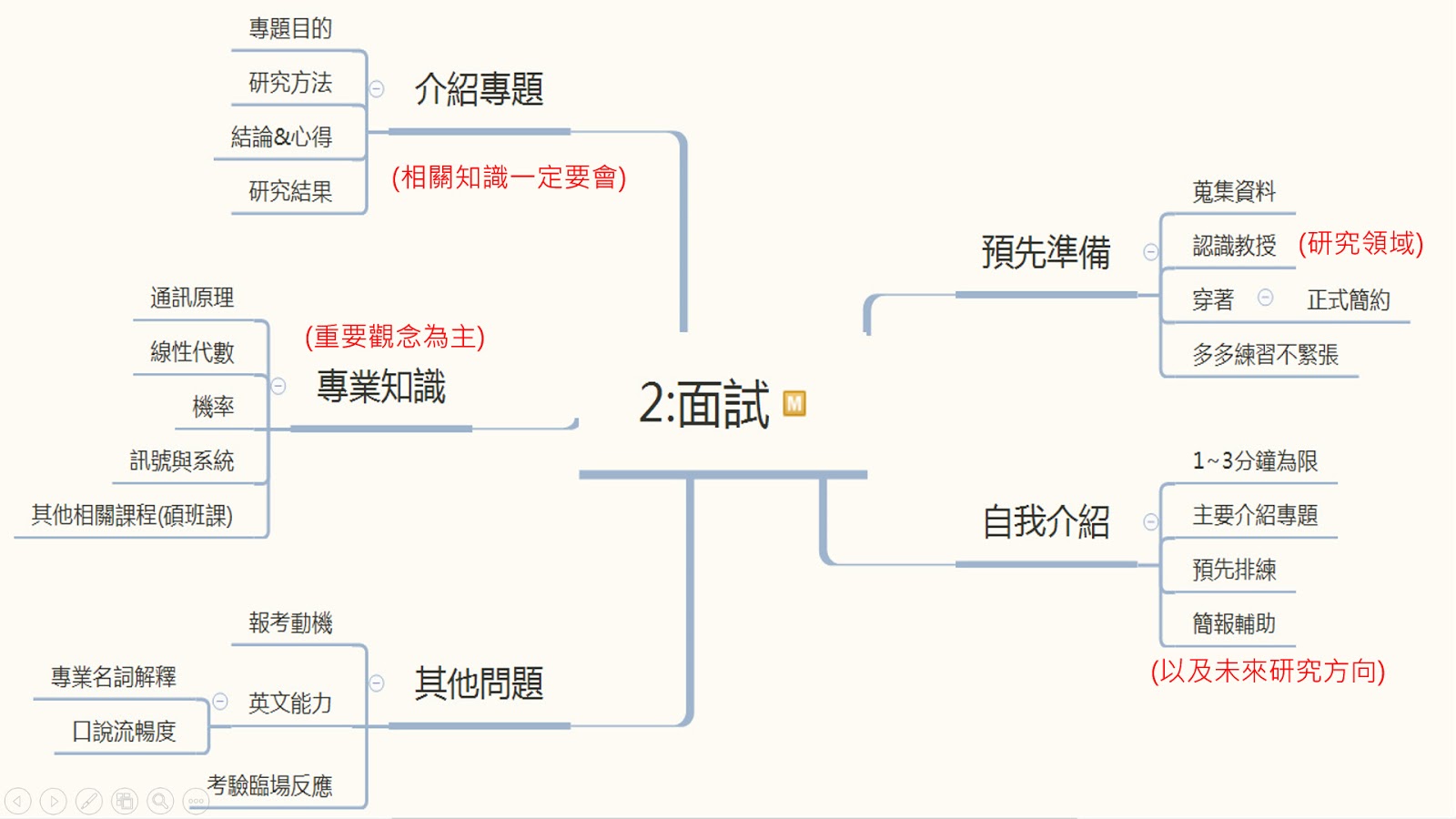
[思路]LeetCode Problems- 617. Merge Two Binary Trees

本篇的問題與處理資料樹狀結構有關,題目原文如下:

Given two binary trees and imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not.

You need to merge them into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of new tree.

Example 1:

Input: 
 Tree 1                     Tree 2                  
          1                         2                             
         / \                       / \                            
        3   2                     1   3                        
       /                           \   \                      
      5                             4   7                  
Output: 
Merged tree:
      3
     / \
    4   5
   / \   \ 
  5   4   7

Note: The merging process must start from the root nodes of both trees.

除此之外,原始程式碼還有附上二元樹的定義:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

二元樹是由節點所組成的有限集合,這個集合若不是空集合,就是由樹根,右子樹(Right subtree)及左子樹(Left subtree)所組合而成.左子樹和右子樹也可以為空集合.

樹中的每一個節點(Node)包含一個項目(如:數字)與兩個指向其他節點的指標

已知原本函式為:

struct TreeNode* mergeTrees(struct TreeNode* t1, struct TreeNode* t2) { }

這個函式要把 t1,t2 兩個子樹做合併,
首先要判斷其中是否有空的子樹,
若其中一棵子樹為空的話則回傳另一棵子樹,
寫成:

if  (!t1)        return t2;
if (!t2)        return t1;

假如兩棵子樹都不為空的話則把其中的值相加,
我們會用運算元 ->  來存取用指標初始化的結構,
寫成:

t1->val =t1->val+ t2->val;

在此把t1+t2的值取代至t1子樹中,因為函式中我們沒辦法新創造一個子樹來存取相加後的值

至於新子樹的左子樹跟右子樹則利用原本函式來做自動重複相加的動作(迭代):

t1->left = mergeTrees(t1->left, t2->left);
t1->right = mergeTrees(t1->right, t2->right);

最後回傳t1子樹,就是相加過後的結果了~!

若有學習過資料結構相關的知識,這一題算是還蠻簡單的