通電技能樹

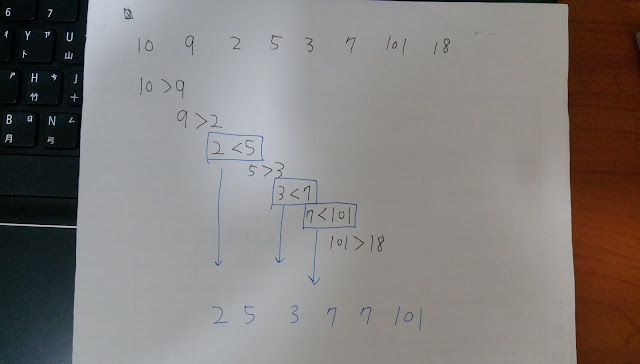
在做完  [思路]LeetCode Problems- 441. Arranging Coins 這題之後 隔天一早十點多起床想說再繼續挑戰一題來試看看 於是按下了LeetCode首頁右下的"Pick One"鍵 跳出了這一題, 原文如下: Given an unsorted array of integers, find the length of longest increasing subsequence. For example, Given  [10, 9, 2, 5, 3, 7, 101, 18] , The longest increasing subsequence is  [2, 3, 7, 101] , therefore the length is  4 . Note that there may be more than one LIS combination, it is only necessary for you to return the length. Your algorithm should run in O( n 2 ) complexity. Follow up:  Could you improve it to O( n  log  n ) time complexity? Credits: Special thanks to  @pbrother  for adding this problem and creating all test cases. 當下看到時有點傻眼 天啊這題目到底想要求甚麼啊~?? 多看幾次才逐漸明瞭 好像是要求這有序數列裡   最長的遞增數列  的個數 如上述那一串數列中,最長的遞增數列為 2 3 7 101  其長度是4 但就數列"內容"來說這不算是唯一的答案, 也應該能寫成2 5 7 101 或者是2 3 7 18 這類 當發覺答案不會是唯一解的時候,其實內心覺得有點怕怕的@@ (心中OS開始 ) 認真在看題目想如何解的時候,腦袋想法變得十分稀少,不知道要如何下手 相信在寫code的初學者或大學生(例如我)...

昨天一早在大學系版上看到教授給學弟妹出的LeetCode練習題, 想說剛畢業沒課的第一天來找點事情做,加上好奇心使然 註冊了網站帳號來看一下題目是甚麼 題目原文是這樣的: You have a total of  n  coins that you want to form in a staircase shape, where every  k -th row must have exactly  k  coins. Given  n , find the total number of  full  staircase rows that can be formed. n  is a non-negative integer and fits within the range of a 32-bit signed integer. Example 1: n = 5 The coins can form the following rows: ¤ ¤ ¤ ¤ ¤ Because the 3rd row is incomplete, we return 2. Example 2: n = 8 The coins can form the following rows: ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Because the 4th row is incomplete, we return 3. 大意是說幾假如給定n枚硬幣,則一共可以排成"完整"階梯的階數是多少, 其中階梯硬幣的排法是 第?階就有?枚硬幣 看題目以及老師FB給的提示, 還必須要把階梯"畫"出來的樣子 一開始看到這個題目時還有點不太知道要從何下手, 但先撇開如何畫階梯這件事情不談, 先只關注輸入的值 n 來下手 [簡化問題] 要如何判斷n枚硬幣是可以排成"完整"階梯狀的數字呢? 不同階數的樓梯,彼此會不會有所關聯呢? 例如一階樓梯 硬幣數是1 二階樓梯 硬幣數是1+2=3 三階樓梯 硬幣數是1+2+3=6 四階硬幣數是1+2+3+4=10  諸如此類... 1 , 3 , 6 , 10 ,......這數列好像有某種...

(此文章僅為個人學習用途並針對書籍做重點整理摘要,若要更多細節,實例與圖示請購買本書支持作者) 第一章:小人退散! *讓看不順眼的人閉嘴 --> 指出對方無意識的習慣動作 ,乍看沒有惡意,但打亂習慣就會打亂一個人的節奏 *讓扯後腿的同事知難而退 -->使自己看起來 高人一等 ,體格壯碩與身材高大的人有"能力很強"的感覺 *對付愛搶功勞的主管 --> 身體接觸 是拉近彼此距離的妙方, 創造肌膚之親例如主動握手或輕輕觸碰肩膀,可以解除警戒心 *馴服個性倔強的下屬 -->把 稍微麻煩的工作 交給他 @自我涉入(self-involvement):讓人覺得有意義,提升自我價值感 *和不對盤的主管建立良好關係 --> 多多打聽主管的個人背景,家庭,個性等相關資訊,清除心中的偏見 @心錨(anchor):大腦對事物的條件反射,會固定人的思考進而影響你的判斷 -->心錨所設定的心理狀態會讓我們憑外表或說話方式來判斷對方 *難搞的主管 -->多 取悅主管 ,使用 "再否定" 的奉承技巧再次否定對方的回應 *做錯事留下好印象 --> 誠心誠意道歉,讓對方留下正面印象 .之後,要 盡量避免與主管接觸(無法避開時則適當保持距離) @理想化(idealiation):讓人留下深刻的第一印象的人,即使之後沒有直接接觸,對方也會逐漸在心中理想化 *讓被動的下屬變得主動積極 -->找到對方的優點,針對優點說出充滿期待的話 @比馬龍效應(Pygmalion effect):自我應驗預言(self-fulfilling prophecy),給予人期望與自信心,則對方也會積極 *讓憤怒的同事冷靜 -->比生氣的人展現出更憤怒的情感 @自我同一性(self-identity):自我認同,讓人將對方的實力與成果錯認為是自己的 *提出無理要求的客戶 -->利用服裝與顏色的威嚴, 黑色西裝 能展現出幹練的形象 *對付喜歡挖苦的人 -->在其面前採取 高壓的態度 或是提高嗓門,就能獲得控制權 *徹底斷絕煩人的推銷或請託 --> 斷然拒絕 才是最不會讓對方感到不愉快...

(此文章僅為個人學習用途並針對書籍做重點整理摘要,若要更多細節,實例與圖示請購買本書支持作者) 第一堂課:邏輯思考並不難!邏輯思考的基礎課程 我希望你不要被他人的教訓束縛.比起任何事物,我最希望你擁有相信自己的內心和直覺的勇氣----Steve Jobs --> 靈感 和 直覺 在商務中不該被捨棄,反而是用來做自己才做得到的工作的重要資產,但重要的是 再試著尋找"深度" [邏輯思考的基礎] *麥肯錫式的真正邏輯思考: 批判性地思考(透過深度洞察,擁有自己的想法) 邏輯性地發展(淺顯易懂地傳達) 思考行為步驟: 自行清楚地確認前提(那是真的~?) 深入調查,傳達根據(因為~,所以那樣) 擁有自己的深入意見(那個意見很好) *邏輯思考的幫助 -->讓各種人站在自己這一邊,獲得許多贊同的重要思考技術 -->使溝通越來越順暢,建立良好的人際關係 *學會邏輯思考不需要腦袋聰明 -->和與生俱來的"腦袋聰明"或"學習力強"無關,任誰都能後天增加邏輯思考能力 *在商務中的必要性:解決課題 試著俯瞰發生在眼前的事 在該狀況中,究竟甚麼是特定的問題 確認特定的問題"是否真的是問題"的根據 擬定解決問題的方案 展開用來實際解決問題的行動 *人的認定或斷定會帶來"不好的事" --> 進一步深入思考"實情是如何?" 能夠防止誤解的認定或斷定所導致的錯誤 例子:購物中心的客訴 ==>試著尋找背後的原因,五花八門的客訴也會有共同的要素 *總是以歸零發想採取行動 -->和處於競爭關係的對手必須在同一個課題上提出"不同的結果"時,除了邏輯思考之外,還需要 創新的發想 -->不要讓過去自己的"思考框架"和"成功體驗"妨礙到你 *只有邏輯性是不夠的 -->有些案例是無論邏輯性再正確,那種思考和行動也並非最佳 --> 批判性思考 不僅在邏輯上是正確的,同時也會產生令人理解,感動人心,切中要點的最佳發想 ...