[思路]LeetCode Problems- 300. Longest Increasing Subsequence
在做完 [思路]LeetCode Problems- 441. Arranging Coins這題之後
隔天一早十點多起床想說再繼續挑戰一題來試看看
於是按下了LeetCode首頁右下的"Pick One"鍵
跳出了這一題,
原文如下:
天啊這題目到底想要求甚麼啊~??
多看幾次才逐漸明瞭
好像是要求這有序數列裡 最長的遞增數列 的個數
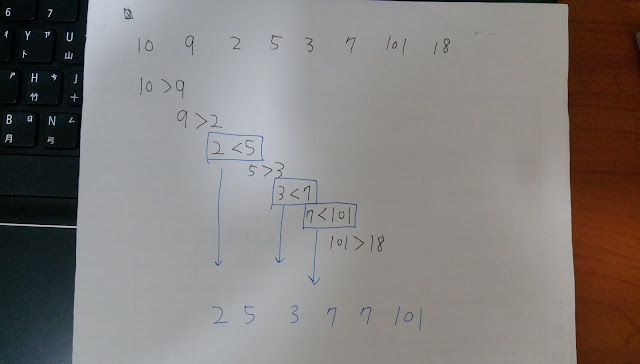
如上述那一串數列中,最長的遞增數列為 2 3 7 101
其長度是4
但就數列"內容"來說這不算是唯一的答案,
也應該能寫成2 5 7 101
或者是2 3 7 18 這類
當發覺答案不會是唯一解的時候,其實內心覺得有點怕怕的@@
(心中OS開始)
認真在看題目想如何解的時候,腦袋想法變得十分稀少,不知道要如何下手
相信在寫code的初學者或大學生(例如我)(專家不算)都會有這種感受
有時候某些題目是我們一眼就可以看出來,找出答案的問題
但卻不曉得要如何描述給冷冰冰的電腦/編譯器聽
在升學教育體制下,我們的大腦被訓練得可說是非常的直覺與快速思考,
但卻很少想過 "思考"的過程/邏輯是如何形塑而成的,
只重視去脈絡化的"答案"
這樣的結果導致於遇到陌生題目時會變得不知所措
要改善的方法
就是認真地回想/recall 解題的過程
發覺自己在邏輯/思考上是否有不足之處
(心中OS結束)
總之,我一開始是想要用最簡單/快速的方法來求出此題的解答
雖然我隱隱約約感覺可能會用到兩個FOR迴圈,但我暫時還是撇開它不管
從最簡單的兩個兩個比較來思考的話,有沒有可能求出答案來呢~?
當時想法是這樣的:
假如我直接兩個兩個元素做比較,若有後一個比前一個大的情況,則得知這兩個元素呈遞增情況,
直接把這兩個元素取出來存進新的vector中
存到新vector後再做一遍,確定這一數列是遞增狀態
全部處理完後若有碰到有相同元素出現
再把它排除掉就好
最後回傳這個vector的大小size()就好了~!
確定乍看之下好像沒什麼大問題後,就開始撰寫程式碼:
vector<int> v1;
for(int i=0; i<=nums.size(); i++){
if (nums[i]<nums[i+1])
{
v1.push_back(nums[i]);
v1.push_back(nums[i+1]);
}//IF
else {}//else
}//for1
for (int k=0;k<v1.size();k++){
if (v1[k]>v1[k+1])
{
std::vector<int>::iterator it = v1.begin()+k;
v1.erase(it);
}//IF2
}//FOR2
//刪掉重複元素
std::vector<int>::iterator eraseit= std::unique(v1.begin(), v1.end()); //排不重覆元素;
v1.erase(eraseit, v1.end()); //沒被排到的刪掉
//for(int j=0; j<v1.size(); j++)
//cout << v1[j] << " ";
return v1.size();
經過測試之後沒發覺問題直接按了送出鍵
孰不知,這就是一連串問題的開始
我在一開始貼出原文時,特別連題目的Credits 都寫出來 不是沒原因的
這個叫做 @pbrother 的人給的特殊case 真的天殺的不是普通特殊,例如:
1.空vector
好吧,那就在多加個判斷式判別好了,總可以了吧
2.一個元素 [0]
好吧,那再多加一個判斷size有沒有大於1 ,總可以了吧
3.重複元素 [2 2]
啥米,還會有重複出現的例子,那再把相鄰元素重複的話去掉,總可以了吧
4. [1 3 2]
....不不不這我就護航不下去了,到底哪裡出問題????
我相信在50%的case中一定都能夠正確運作,但總是難免會有50%的例外狀況啊~
(OS:明明自己邏輯不好還怪Credits的人)
結果這樣子東改西改把例外情況改掉,
整個程式的走向到最後連自己都不曉得改錯了甚麼.....
心力交瘁的情況下
只好先擱在一旁明天再繼續想
(隔天早上)
我回顧了一下我的邏輯,老實說的確是十分粗糙又不嚴謹,
所以我決定全部打掉重來,改用雙重FOR迴圈來撰寫
將原本程式碼寫成:
for (int i=0;i<nums.size()-1;i++){
for (int j=0;j<i;j++){
if (nums[j]>=nums[i])
{
vector<int>::iterator k = nums.begin()+j;
nums.erase(k);
}
}
}
這一段雙重FOR迴圈的意思是說,
要確保數列中的"前一個元素"要小於"後一個元素"
假如"前一個元素"有大於"後一個元素",則這前一個元素會被刪除,
確保數列一定要呈現由小到大的狀態
for (int q=0;q<nums.size();q++){
if (nums[q]>nums[q+1])
{
//刪掉q+1
vector<int>::iterator k2 = nums.begin()+(q+1);
nums.erase(k2);
}
}
return nums.size();
這裡的第二個FOR則是為了要做檢查尾端,
因為萬一尾端的數字比前一個還要小的話則會不小心刪掉前一個數字,導致數列最後尾端的字沒有符合規律
這第二個寫法(應該)比第一種寫法還要簡潔一點,
畢竟沒有多增加新的vector,造成多餘的計算量
接著再加上一些判斷條件(不為空向量&長度大於1)之後,重新再跑跑看.....
出現一個意想不到的問題
居然輸入一個長達2500個元素的向量,程式居然會跑不起來
這時我已經發覺,目前這狀況,似乎不是跟邏輯之類的有關係了
反而是程式運算量負荷不了的問題
這不得不讓我重新思考精簡程式的方法
假如若要再用更好的方法來運算的話,那就要不單單用for if while這些語法來做最好的方案就是直接用C++內的STL庫,例如<algorithm>
那有沒有一個函式,可以用來找數列中的元素,做類似比大小的事情呢...?
.
.
.
結果仔細一查還真的有相關的function,
盛重介紹: lower_bound用法
std::lower_bound(迭代子1,迭代子2,想插入的數字假設為3)
這個函數的用法在於,它可以找出在一個有順序的數列中,找出一個可以安插3的位置
使其能大於等於前一個元素假設現在有一數列如下:
4 10 11 30 69 70 96 100
我們把這數列存入vector中,命為v1
則第一個位置可以用v1.begin()表示最後一個位置可以用v1.end()表示
若我們給定數字叫做12好了則12可以被插入數列哪個位置,使其能夠大於前面的數字呢?
應該是原本數列放30的那個位置對吧~
故求法就能寫成:
std::vector<int>::iterator it = std::lower_bound(v1.begin(), v1.end(), 12);
這個it迭代子,會指向原本數列中存放30的那個位置這個位置沒辦法單純用cout輸出來看,但可以利用其類似於指標的特性
在編譯器上寫
cout<< *it <<endl; //存取出vector元素則會輸出其結果為 30 也就是數列第4個位置,可以插入12
有了這個function,則我就可以把整個程式又一次大幅簡化
最後寫成如下結果:
vector<int> v1; //先定義一個空向量
for (int i = 0; i<nums.size(); i++) {
std::vector<int>::iterator it;
it = lower_bound(v1.begin(), v1.end(), nums[i]); //在v1中適合插入nums[i]數字的位置
if (it == v1.end()) //假如指向最後一個位置,代表原v1中的數字都比nums[i]還小
{
v1.push_back(nums[i]); //其數字直接存入v1,成遞增狀態
}
else //假如不是為空,代表原v1中的數字比nums[i]還要大
{
*it = nums[i]; //利用類似指標的特性,把原v1中的數字直接取代掉
}
這樣直接看可能不太能理解,直接在紙上畫圖示範:
注意的是,vector的end()指的是vector 最尾端元素的下一個位置不代表最末元素,所以可以利用這特性
這樣做下來就可以確保是一個最長遞增的數列了
再加上一些判斷條件(不為空向量&長度大於1)之後,重新再跑跑看.....成功! .

這次算是有進步吧哈哈~ヾ(*´∇`)ノ
總覺得寫到最後反而是要練習vector的用法,以及利用其迭代子的特性
就可以順利解出這題
隔天一早十點多起床想說再繼續挑戰一題來試看看
於是按下了LeetCode首頁右下的"Pick One"鍵
跳出了這一題,
原文如下:
Given an unsorted array of integers, find the length of longest increasing subsequence.
For example,
Given
The longest increasing subsequence is
Given
[10, 9, 2, 5, 3, 7, 101, 18],The longest increasing subsequence is
[2, 3, 7, 101], therefore the length is 4. Note that there may be more than one LIS combination, it is only necessary for you to return the length.
Your algorithm should run in O(n2) complexity.
Follow up: Could you improve it to O(n log n) time complexity?
當下看到時有點傻眼天啊這題目到底想要求甚麼啊~??
多看幾次才逐漸明瞭
好像是要求這有序數列裡 最長的遞增數列 的個數
如上述那一串數列中,最長的遞增數列為 2 3 7 101
其長度是4
但就數列"內容"來說這不算是唯一的答案,
也應該能寫成2 5 7 101
或者是2 3 7 18 這類
當發覺答案不會是唯一解的時候,其實內心覺得有點怕怕的@@
(心中OS開始)
認真在看題目想如何解的時候,腦袋想法變得十分稀少,不知道要如何下手
相信在寫code的初學者或大學生(例如我)(專家不算)都會有這種感受
有時候某些題目是我們一眼就可以看出來,找出答案的問題
但卻不曉得要如何描述給冷冰冰的電腦/編譯器聽
在升學教育體制下,我們的大腦被訓練得可說是非常的直覺與快速思考,
但卻很少想過 "思考"的過程/邏輯是如何形塑而成的,
只重視去脈絡化的"答案"
這樣的結果導致於遇到陌生題目時會變得不知所措
要改善的方法
就是認真地回想/recall 解題的過程
發覺自己在邏輯/思考上是否有不足之處
(心中OS結束)
總之,我一開始是想要用最簡單/快速的方法來求出此題的解答
雖然我隱隱約約感覺可能會用到兩個FOR迴圈,但我暫時還是撇開它不管
從最簡單的兩個兩個比較來思考的話,有沒有可能求出答案來呢~?
當時想法是這樣的:
假如我直接兩個兩個元素做比較,若有後一個比前一個大的情況,則得知這兩個元素呈遞增情況,
直接把這兩個元素取出來存進新的vector中
存到新vector後再做一遍,確定這一數列是遞增狀態
全部處理完後若有碰到有相同元素出現
再把它排除掉就好
最後回傳這個vector的大小size()就好了~!
確定乍看之下好像沒什麼大問題後,就開始撰寫程式碼:
vector<int> v1;
for(int i=0; i<=nums.size(); i++){
if (nums[i]<nums[i+1])
{
v1.push_back(nums[i]);
v1.push_back(nums[i+1]);
}//IF
else {}//else
}//for1
for (int k=0;k<v1.size();k++){
if (v1[k]>v1[k+1])
{
std::vector<int>::iterator it = v1.begin()+k;
v1.erase(it);
}//IF2
}//FOR2
//刪掉重複元素
std::vector<int>::iterator eraseit= std::unique(v1.begin(), v1.end()); //排不重覆元素;
v1.erase(eraseit, v1.end()); //沒被排到的刪掉
//for(int j=0; j<v1.size(); j++)
//cout << v1[j] << " ";
return v1.size();
經過測試之後沒發覺問題直接按了送出鍵
孰不知,這就是一連串問題的開始
我在一開始貼出原文時,特別連題目的Credits 都寫出來 不是沒原因的
這個叫做 @pbrother 的人給的特殊case 真的
1.空vector
好吧,那就在多加個判斷式判別好了,總可以了吧
2.一個元素 [0]
好吧,那再多加一個判斷size有沒有大於1 ,總可以了吧
3.重複元素 [2 2]
啥米,還會有重複出現的例子,那再把相鄰元素重複的話去掉,總可以了吧
4. [1 3 2]
....不不不這我就護航不下去了,到底哪裡出問題????
我相信在50%的case中一定都能夠正確運作,但總是難免會有50%的例外狀況啊~
(OS:明明自己邏輯不好還怪Credits的人)
結果這樣子東改西改把例外情況改掉,
整個程式的走向到最後連自己都不曉得改錯了甚麼.....
心力交瘁的情況下
只好先擱在一旁明天再繼續想
(隔天早上)
我回顧了一下我的邏輯,老實說的確是十分粗糙又不嚴謹,
所以我決定全部打掉重來,改用雙重FOR迴圈來撰寫
將原本程式碼寫成:
for (int i=0;i<nums.size()-1;i++){
for (int j=0;j<i;j++){
if (nums[j]>=nums[i])
{
vector<int>::iterator k = nums.begin()+j;
nums.erase(k);
}
}
}
這一段雙重FOR迴圈的意思是說,
要確保數列中的"前一個元素"要小於"後一個元素"
假如"前一個元素"有大於"後一個元素",則這前一個元素會被刪除,
確保數列一定要呈現由小到大的狀態
for (int q=0;q<nums.size();q++){
if (nums[q]>nums[q+1])
{
//刪掉q+1
vector<int>::iterator k2 = nums.begin()+(q+1);
nums.erase(k2);
}
}
return nums.size();
這裡的第二個FOR則是為了要做檢查尾端,
因為萬一尾端的數字比前一個還要小的話則會不小心刪掉前一個數字,導致數列最後尾端的字沒有符合規律
這第二個寫法(應該)比第一種寫法還要簡潔一點,
畢竟沒有多增加新的vector,造成多餘的計算量
接著再加上一些判斷條件(不為空向量&長度大於1)之後,重新再跑跑看.....
出現一個意想不到的問題
居然輸入一個長達2500個元素的向量,程式居然會跑不起來
這時我已經發覺,目前這狀況,似乎不是跟邏輯之類的有關係了
反而是程式運算量負荷不了的問題
這不得不讓我重新思考精簡程式的方法
假如若要再用更好的方法來運算的話,那就要不單單用for if while這些語法來做最好的方案就是直接用C++內的STL庫,例如<algorithm>
那有沒有一個函式,可以用來找數列中的元素,做類似比大小的事情呢...?
.
.
.
結果仔細一查還真的有相關的function,
盛重介紹: lower_bound用法
std::lower_bound(迭代子1,迭代子2,想插入的數字假設為3)
這個函數的用法在於,它可以找出在一個有順序的數列中,找出一個可以安插3的位置
使其能大於等於前一個元素假設現在有一數列如下:
4 10 11 30 69 70 96 100
我們把這數列存入vector中,命為v1
則第一個位置可以用v1.begin()表示最後一個位置可以用v1.end()表示
若我們給定數字叫做12好了則12可以被插入數列哪個位置,使其能夠大於前面的數字呢?
應該是原本數列放30的那個位置對吧~
故求法就能寫成:
std::vector<int>::iterator it = std::lower_bound(v1.begin(), v1.end(), 12);
這個it迭代子,會指向原本數列中存放30的那個位置這個位置沒辦法單純用cout輸出來看,但可以利用其類似於指標的特性
在編譯器上寫
cout<< *it <<endl; //存取出vector元素則會輸出其結果為 30 也就是數列第4個位置,可以插入12
有了這個function,則我就可以把整個程式又一次大幅簡化
最後寫成如下結果:
vector<int> v1; //先定義一個空向量
for (int i = 0; i<nums.size(); i++) {
std::vector<int>::iterator it;
it = lower_bound(v1.begin(), v1.end(), nums[i]); //在v1中適合插入nums[i]數字的位置
if (it == v1.end()) //假如指向最後一個位置,代表原v1中的數字都比nums[i]還小
{
v1.push_back(nums[i]); //其數字直接存入v1,成遞增狀態
}
else //假如不是為空,代表原v1中的數字比nums[i]還要大
{
*it = nums[i]; //利用類似指標的特性,把原v1中的數字直接取代掉
}
這樣直接看可能不太能理解,直接在紙上畫圖示範:
注意的是,vector的end()指的是vector 最尾端元素的下一個位置不代表最末元素,所以可以利用這特性
這樣做下來就可以確保是一個最長遞增的數列了
再加上一些判斷條件(不為空向量&長度大於1)之後,重新再跑跑看.....成功! .

這次算是有進步吧哈哈~ヾ(*´∇`)ノ
總覺得寫到最後反而是要練習vector的用法,以及利用其迭代子的特性
就可以順利解出這題








留言
張貼留言